Periodic boundary conditions and their implementation in ABAQUS

1 Introduction

Periodic boundary conditions (PBCs) are an essential tool in computational mechanics, particularly for simulating materials with repeating microstructures. They are commonly used in modelling representative volume elements (RVEs) of heterogeneous materials, such as composites, polycrystals, and foams.

In this blog, we shall discuss:

• the concept behind periodic boundary conditions,
• the derivation of periodic constraints for a unit cell, and
• their practical implementation in ABAQUS finite element software using the equation constraint option.

---

2 Concept of periodic boundary conditions

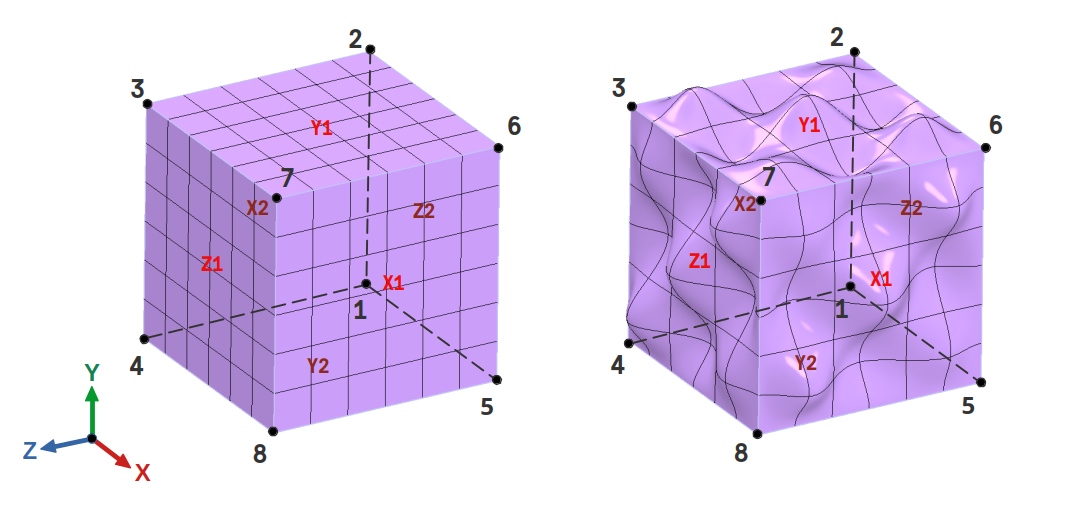Figure 1: Initial configuration(left) and Final configuration(right)

To apply periodic BCs, the chosen RVE must allow being stacked together to form a macroscopic body with a periodic structure. One example of such an RVE is a cuboid unit cell as shown in Figure 1. Figure 1 (right) represents the RVE in its final configuration after the application of periodic boundary conditions.

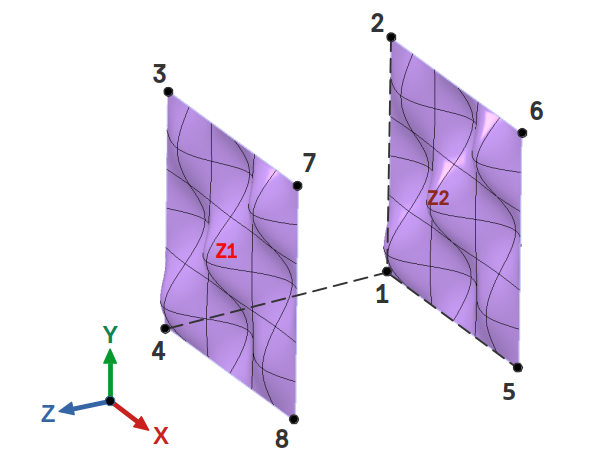Figure 2: Two opposite faces $Z1$ and $Z2$ in final configuration.

All the 6 faces can be grouped into 3 pairs, in which each pair contains two opposite faces. The (Figure 2) shows two opposite faces $Z1$ and $Z2$ in final configuration. In each pair, the two faces of the RVE must be related to each other in such a way that they follow the same displacement pattern i.e., the faces should perfectly overlap each other. This is achieved by tying the related DOF together i.e., the difference between the displacements of two opposite faces must be a constant vector. This is expressed for all 3 pairs in the following 3 sets of equations

\[\begin{align} \mathbf u^{X1} - \mathbf u^{X2} &= \mathbf p \\ \mathbf u^{Y1} - \mathbf u^{Y2} &= \mathbf q \\ \mathbf u^{Z1} - \mathbf u^{Z2} &= \mathbf r \end{align}\]

where $\mathbf p, \mathbf q, \mathbf r$ are constant vectors

---

3 Derivation of constraint equations

In a finite element mesh, the domain is discretized into elements. As a result, the nodes at corners are shared between 3 faces and the nodes on the edges are shared between two faces. This would lead to some redundant constraints on the shared nodes in the above set of equations $(1)-(3)$. These redundant equations can be eliminated by separating the equations $(1)-(3)$ into 3 distinct sets for corners, inner nodes of edges and inner nodes of faces.

For the faces $Z1$ and $Z2$, the equations $(3)$ can be separated as

\[\begin{align*} \mathbf u^{4873} - \mathbf u^{1562} &= \mathbf r \end{align*} \quad\quad \text{for inner nodes of faces}\] \[\begin{align*} \mathbf u^{48} - \mathbf u^{15} &= \mathbf r \\ \mathbf u^{87} - \mathbf u^{56} &= \mathbf r \\ \mathbf u^{73} - \mathbf u^{62} &= \mathbf r \\ \mathbf u^{34} - \mathbf u^{21} &= \mathbf r \end{align*}\quad\quad\text{for inner nodes of edges}\] \[\begin{align*} \mathbf u^{4} - \mathbf u^{1} &= \mathbf r \\ \mathbf u^{8} - \mathbf u^{5} &= \mathbf r \\ \mathbf u^{7} - \mathbf u^{6} &= \mathbf r \\ \mathbf u^{3} - \mathbf u^{2} &= \mathbf r \end{align*}\quad\quad\text{for corner nodes}\]

Similarly, equations $(2),(3)$ can also be separated for corners, edges and faces. The complete sets of equations are given below

3.1 Set-I (corner nodes)

For the faces $X^+$ and $X^-$

\[\begin{align} \mathbf u^{5} - \mathbf u^{1} &= \mathbf p \\ \mathbf u^{6} - \mathbf u^{2} &= \mathbf p \\ \mathbf u^{7} - \mathbf u^{3} &= \mathbf p \\ \mathbf u^{8} - \mathbf u^{4} &= \mathbf p \\ \end{align}\]

For the faces $Y^+$ and $Y^-$

\[\begin{align} \mathbf u^{2} - \mathbf u^{1} &= \mathbf q \\ \mathbf u^{3} - \mathbf u^{4} &= \mathbf q \\ \mathbf u^{7} - \mathbf u^{8} &= \mathbf q \\ \mathbf u^{6} - \mathbf u^{5} &= \mathbf q \end{align}\]

For the faces $Z^+$ and $Z^-$

\[\begin{align} \mathbf u^{4} - \mathbf u^{1} &= \mathbf r \\ \mathbf u^{8} - \mathbf u^{5} &= \mathbf r \\ \mathbf u^{7} - \mathbf u^{6} &= \mathbf r \\ \mathbf u^{3} - \mathbf u^{2} &= \mathbf r \end{align}\] \[\begin{align*} (4)&\implies\mathbf u^{5} - \mathbf u^{1} = \mathbf p \\ (5)&\implies\mathbf u^{6} - \mathbf u^{2} = \mathbf p \implies \mathbf u^{6} - \mathbf u^{2} = \mathbf u^{5} - \mathbf u^{1} \\ (6)&\implies\mathbf u^{7} - \mathbf u^{3} = \mathbf p \implies \mathbf u^{7} - \mathbf u^{3} = \mathbf u^{5} - \mathbf u^{1} \\ (7)&\implies\mathbf u^{8} - \mathbf u^{4} = \mathbf p \implies \mathbf u^{8} - \mathbf u^{4} = \mathbf u^{5} - \mathbf u^{1} \end{align*}\] \[\begin{align*} (8)&\implies\mathbf u^{2} - \mathbf u^{1} = \mathbf q \\ (9)&\implies\mathbf u^{3} - \mathbf u^{4} = \mathbf q \implies \mathbf u^{3} - \mathbf u^{4} = \mathbf u^{2} - \mathbf u^{1}\\ (10)&\implies\mathbf u^{7} - \mathbf u^{8} = \mathbf q \implies \mathbf u^{7} - \mathbf u^{8} = \mathbf u^{3} - \mathbf u^{4} \implies \mathbf u^{7} - \mathbf u^{3} = \mathbf u^{8} - \mathbf u^{4} \implies \mathbf u^{7} - \mathbf u^{3} = \mathbf u^{5} - \mathbf u^{1}\implies(6)\quad\text{redundant}\\ (11)&\implies\mathbf u^{6} - \mathbf u^{5} = \mathbf q \implies \mathbf u^{6} - \mathbf u^{5} = \mathbf u^{2} - \mathbf u^{1}\implies \mathbf u^{6} - \mathbf u^{2} = \mathbf u^{5} - \mathbf u^{1} \implies (5)\quad\text{redundant}\\ \end{align*}\] \[\begin{align*} (12)&\implies\mathbf u^{4} - \mathbf u^{1} = \mathbf r \\ (13)&\implies\mathbf u^{8} - \mathbf u^{5} = \mathbf r \implies \mathbf u^{8} - \mathbf u^{5} = \mathbf u^{4} - \mathbf u^{1}\implies \mathbf u^{8} - \mathbf u^{4} = \mathbf u^{5} - \mathbf u^{1}\implies(7)\quad\text{redundant}\\ (14)&\implies\mathbf u^{7} - \mathbf u^{6} = \mathbf r \implies \mathbf u^{7} - \mathbf u^{6} = \mathbf u^{3} - \mathbf u^{2}\implies \mathbf u^{7} - \mathbf u^{3} = \mathbf u^{6} - \mathbf u^{2}\implies \mathbf u^{7} - \mathbf u^{3} = \mathbf u^{5} - \mathbf u^{1}\implies(6)\quad\text{redundant}\\ (15)&\implies\mathbf u^{3} - \mathbf u^{2} = \mathbf r \implies \mathbf u^{3} - \mathbf u^{2} = \mathbf u^{4} - \mathbf u^{1} \implies \mathbf u^{3} - \mathbf u^{4} = \mathbf u^{2} - \mathbf u^{1}\implies(9)\quad\text{redundant} \end{align*}\]

The remaining equations in Set-I are

\[\begin{align*} (5)&\implies \mathbf u^{6} - \mathbf u^{2} = \mathbf u^{5} - \mathbf u^{1} \\ (6)&\implies \mathbf u^{7} - \mathbf u^{3} = \mathbf u^{5} - \mathbf u^{1} \\ (7)&\implies \mathbf u^{8} - \mathbf u^{4} = \mathbf u^{5} - \mathbf u^{1} \\ (9)&\implies \mathbf u^{3} - \mathbf u^{4} = \mathbf u^{2} - \mathbf u^{1} \\ \end{align*}\] \[\begin{align*} (4)&\implies\mathbf u^{5} - \mathbf u^{1} = \mathbf p \\ (8)&\implies\mathbf u^{2} - \mathbf u^{1} = \mathbf q \\ (12)&\implies\mathbf u^{4} - \mathbf u^{1} = \mathbf r \\ \end{align*}\]

3.2 Set-II (inner nodes of edges)

For the faces $X^+$ and $X^-$

\[\begin{align} \mathbf u^{56} - \mathbf u^{12} &= \mathbf p \\ \mathbf u^{67} - \mathbf u^{23} &= \mathbf p \\ \mathbf u^{78} - \mathbf u^{34} &= \mathbf p \\ \mathbf u^{85} - \mathbf u^{41} &= \mathbf p \\ \end{align}\]

For the faces $Y^+$ and $Y^-$

\[\begin{align} \mathbf u^{23} - \mathbf u^{14} &= \mathbf q \\ \mathbf u^{37} - \mathbf u^{48} &= \mathbf q \\ \mathbf u^{76} - \mathbf u^{85} &= \mathbf q \\ \mathbf u^{62} - \mathbf u^{51} &= \mathbf q \\ \end{align}\]

For the faces $Z^+$ and $Z^-$

\[\begin{align} \mathbf u^{48} - \mathbf u^{15} &= \mathbf r \\ \mathbf u^{87} - \mathbf u^{56} &= \mathbf r \\ \mathbf u^{73} - \mathbf u^{62} &= \mathbf r \\ \mathbf u^{34} - \mathbf u^{21} &= \mathbf r \\ \end{align}\] \[\begin{align*} (16)&\implies\mathbf u^{56} - \mathbf u^{12} = \mathbf u^{5} - \mathbf u^{1} \\ (17)&\implies\mathbf u^{67} - \mathbf u^{23} = \mathbf u^{5} - \mathbf u^{1} = \mathbf u^{85} - \mathbf u^{41} \implies \mathbf u^{67} - \mathbf u^{85} = \mathbf u^{23} - \mathbf u^{41}\implies \mathbf u^{67} - \mathbf u^{85} = \mathbf u^{2} - \mathbf u^{1}\implies(22)\quad\text{redundant}\\ (18)&\implies\mathbf u^{78} - \mathbf u^{34} = \mathbf u^{5} - \mathbf u^{1} \\ (19)&\implies\mathbf u^{85} - \mathbf u^{41} = \mathbf u^{5} - \mathbf u^{1} \\ \end{align*}\] \[\begin{align*} (20)&\implies\mathbf u^{23} - \mathbf u^{14} = \mathbf u^{2} - \mathbf u^{1} \\ (21)&\implies\mathbf u^{37} - \mathbf u^{48} = \mathbf u^{2} - \mathbf u^{1} = \mathbf u^{62} - \mathbf u^{51}\implies\mathbf u^{37} - \mathbf u^{62} = \mathbf u^{48} - \mathbf u^{51} \implies\mathbf u^{37} - \mathbf u^{62} = \mathbf u^{4} - \mathbf u^{1} \implies (26)\quad\text{redundant}\\ (22)&\implies\mathbf u^{76} - \mathbf u^{85} = \mathbf u^{2} - \mathbf u^{1} \\ (23)&\implies\mathbf u^{62} - \mathbf u^{51} = \mathbf u^{2} - \mathbf u^{1} \\ \end{align*}\] \[\begin{align*} (24)&\implies\mathbf u^{48} - \mathbf u^{15} = \mathbf u^{4} - \mathbf u^{1} \\ (25)&\implies\mathbf u^{87} - \mathbf u^{56} = \mathbf u^{4} - \mathbf u^{1} = \mathbf u^{34} - \mathbf u^{21} \implies\mathbf u^{87} - \mathbf u^{34} = \mathbf u^{56} - \mathbf u^{21} \implies\mathbf u^{87} - \mathbf u^{34} = \mathbf u^{5} - \mathbf u^{1}\implies(18)\quad\text{redundant}\\ (26)&\implies\mathbf u^{73} - \mathbf u^{62} = \mathbf u^{4} - \mathbf u^{1} \\ (27)&\implies\mathbf u^{34} - \mathbf u^{21} = \mathbf u^{4} - \mathbf u^{1} \\ \end{align*}\]

The remaining equations in Set-II are

\[\begin{align*} (16)&\implies\mathbf u^{56} - \mathbf u^{12} = \mathbf u^{5} - \mathbf u^{1} \\ (18)&\implies\mathbf u^{78} - \mathbf u^{34} = \mathbf u^{5} - \mathbf u^{1} \\ (19)&\implies\mathbf u^{85} - \mathbf u^{41} = \mathbf u^{5} - \mathbf u^{1} \\ \end{align*}\] \[\begin{align*} (20)&\implies\mathbf u^{23} - \mathbf u^{14} = \mathbf u^{2} - \mathbf u^{1} \\ (22)&\implies\mathbf u^{76} - \mathbf u^{85} = \mathbf u^{2} - \mathbf u^{1} \\ (23)&\implies\mathbf u^{62} - \mathbf u^{51} = \mathbf u^{2} - \mathbf u^{1} \\ \end{align*}\] \[\begin{align*} (24)&\implies\mathbf u^{48} - \mathbf u^{15} = \mathbf u^{4} - \mathbf u^{1} \\ (26)&\implies\mathbf u^{73} - \mathbf u^{62} = \mathbf u^{4} - \mathbf u^{1} \\ (27)&\implies\mathbf u^{34} - \mathbf u^{21} = \mathbf u^{4} - \mathbf u^{1} \\ \end{align*}\]

3.3 Set-III (inner nodes of faces)

\[\begin{align*} \mathbf u^{5678} - \mathbf u^{1234} &= \mathbf p \implies \mathbf u^{5678} - \mathbf u^{1234} = \mathbf u^{5} - \mathbf u^{1}\quad \because \text{from eq(4)}\\ \mathbf u^{2376} - \mathbf u^{1485} &= \mathbf q \implies \mathbf u^{2376} - \mathbf u^{1485} = \mathbf u^{2} - \mathbf u^{1}\quad \because \text{from eq(8)}\\ \mathbf u^{4873} - \mathbf u^{1562} &= \mathbf r\implies \mathbf u^{4873} - \mathbf u^{1562} = \mathbf u^{4} - \mathbf u^{1}\quad \because \text{from eq(12)} \end{align*}\]

---

4 The final complete list of constraint equations

Set-I (corners)

\[\begin{align*} \mathbf u^{6} - \mathbf u^{2} &= \mathbf u^{5}- \mathbf u^{1} \\ \mathbf u^{7} - \mathbf u^{3} &= \mathbf u^{5}- \mathbf u^{1} \\ \mathbf u^{8} - \mathbf u^{4} &= \mathbf u^{5}- \mathbf u^{1} \\ \mathbf u^{3} - \mathbf u^{4} &= \mathbf u^{2}- \mathbf u^{1} \\ \end{align*}\]

Set-II (edges)

\[\begin{align*} \mathbf u^{56} - \mathbf u^{12} = \mathbf u^{5} - \mathbf u^{1} \\ \mathbf u^{78} - \mathbf u^{34} = \mathbf u^{5} - \mathbf u^{1} \\ \mathbf u^{85} - \mathbf u^{41} = \mathbf u^{5} - \mathbf u^{1} \\ \end{align*}\] \[\begin{align*} \mathbf u^{23} - \mathbf u^{14} = \mathbf u^{2} - \mathbf u^{1} \\ \mathbf u^{76} - \mathbf u^{85} = \mathbf u^{2} - \mathbf u^{1} \\ \mathbf u^{62} - \mathbf u^{51} = \mathbf u^{2} - \mathbf u^{1} \\ \end{align*}\] \[\begin{align*} \mathbf u^{48} - \mathbf u^{15} = \mathbf u^{4} - \mathbf u^{1} \\ \mathbf u^{73} - \mathbf u^{62} = \mathbf u^{4} - \mathbf u^{1} \\ \mathbf u^{34} - \mathbf u^{21} = \mathbf u^{4} - \mathbf u^{1} \\ \end{align*}\]

Set-III (faces)

\[\begin{align*} \mathbf u^{5678} - \mathbf u^{1234} = \mathbf u^{5} - \mathbf u^{1}\\ \mathbf u^{2376} - \mathbf u^{1485} = \mathbf u^{2} - \mathbf u^{1}\\ \mathbf u^{4873} - \mathbf u^{1562} = \mathbf u^{4} - \mathbf u^{1} \end{align*}\]

---

5 Prescribing displacement boundary conditions

The above set of equations constrain the degrees of freedom of all the boundary nodes except $5, 2, 4, 1$. Hence, the displacement boundary conditions for the periodic RVE are set by prescribing displacement of the corner nodes $5, 2, 4$ whereas node $1$ is constrained to avoid rigid body translations. The equations $(4), (8), (12)$ can be written as follows

\[\begin{align*} (4)&\implies\mathbf u^{5} - \mathbf u^{1} = \mathbf p &\implies\mathbf u^{5} = \mathbf p\\ (8)&\implies\mathbf u^{2} - \mathbf u^{1} = \mathbf q &\implies\mathbf u^{2} = \mathbf q \\ (12)&\implies\mathbf u^{4} - \mathbf u^{1} = \mathbf r &\implies\mathbf u^{4} = \mathbf r\\ \end{align*}\quad\quad\because\mathbf u^1=\mathbf 0\]

Above set of equations can be expressed in matrix form as

\[\begin{equation} \implies \begin{bmatrix} u^5 & u^{2} & u^4 \\ v^5 & v^{2} & v^4 \\ w^5 & w^{2} & w^4 \\ \end{bmatrix}= \begin{bmatrix} p_1 & q_1 & r_1 \\ p_2 & q_2 & r_2 \\ p_3 & q_3 & r_3 \\ \end{bmatrix} = \nabla\mathbf{u}\times\text{size of RVE} \end{equation}\]

where $u,v$ and $w$ are the displacements along $X,Y$ and $Z$ directions respectively. The above matrix is equivalent to the displacement gradient tensor multiplied by size of the RVE.

---

6 Boundary conditions: examples

6.1 Homogenization

The calculation of the homogenized elastic stiffness tensor requires solving six boundary value problems with six distinct strain boundary conditions: three uniaxial strains along the $X$, $Y$, and $Z$ axes and three pure shear strains in the $XY$, $YZ$, and $XZ$ planes. For each boundary value problem, the average stress response of the RVE is determined. Using Hooke’s law, the average stress and the average strain (i.e., the applied strain) yield a single column of the elastic stiffness matrix. The following is the list of 6 boundary conditions with $a$ as prescribed displacement.

Uniaxial strain along X-axis

\[\begin{bmatrix} u^5 & u^{2} & u^4 \\ v^5 & v^{2} & v^4 \\ w^5 & w^{2} & w^4 \\ \end{bmatrix}= \begin{bmatrix} a & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} \quad\text{and}\quad\mathbf u^1 = \mathbf 0\]

Uniaxial strain along Y-axis

\[\begin{bmatrix} u^5 & u^{2} & u^4 \\ v^5 & v^{2} & v^4 \\ w^5 & w^{2} & w^4 \\ \end{bmatrix}= \begin{bmatrix} 0 & 0 & 0 \\ 0 & a & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} \quad\text{and}\quad\mathbf u^1 = \mathbf 0\]

Uniaxial strain along Z-axis

\[\begin{bmatrix} u^5 & u^{2} & u^4 \\ v^5 & v^{2} & v^4 \\ w^5 & w^{2} & w^4 \\ \end{bmatrix}= \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & a \\ \end{bmatrix} \quad\text{and}\quad\mathbf u^1 = \mathbf 0\]

Pure shear strain in YZ-plane

\[\begin{bmatrix} u^5 & u^{2} & u^4 \\ v^5 & v^{2} & v^4 \\ w^5 & w^{2} & w^4 \\ \end{bmatrix}= \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & a \\ 0 & a & 0 \\ \end{bmatrix} \quad\text{and}\quad\mathbf u^1 = \mathbf 0\]

Pure shear strain in XZ-plane

\[\begin{bmatrix} u^5 & u^{2} & u^4 \\ v^5 & v^{2} & v^4 \\ w^5 & w^{2} & w^4 \\ \end{bmatrix}= \begin{bmatrix} 0 & 0 & a\\ 0 & 0 & 0 \\ a & 0 & 0 \\ \end{bmatrix} \quad\text{and}\quad\mathbf u^1 = \mathbf 0\]

Pure shear strain in XY-Plane

\[\begin{bmatrix} u^5 & u^{2} & u^4 \\ v^5 & v^{2} & v^4 \\ w^5 & w^{2} & w^4 \\ \end{bmatrix}= \begin{bmatrix} 0 & a & 0 \\ a & 0 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} \quad\text{and}\quad\mathbf u^1 = \mathbf 0\]

---

6.2 Isochoric boundary conditions

The following boundary conditions result in a deformation with no change in volume.

Tension along X-axis

\[\begin{bmatrix} u^5 & u^{2} & u^4 \\ v^5 & v^{2} & v^4 \\ w^5 & w^{2} & w^4 \\ \end{bmatrix}= \begin{bmatrix} a & 0 & 0 \\ 0 & -a/2 & 0 \\ 0 & 0 & -a/2 \\ \end{bmatrix} \quad\text{and}\quad\mathbf u^1 = \mathbf 0\]

Simple shear in XZ-Plane

\[\begin{bmatrix} u^5 & u^{2} & u^4 \\ v^5 & v^{2} & v^4 \\ w^5 & w^{2} & w^4 \\ \end{bmatrix}= \begin{bmatrix} 0 & 0 & a \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} \quad\text{and}\quad\mathbf u^1 = \mathbf 0\]

Pure shear in XZ-Plane

\[\begin{bmatrix} u^5 & u^{2} & u^4 \\ v^5 & v^{2} & v^4 \\ w^5 & w^{2} & w^4 \\ \end{bmatrix}= \begin{bmatrix} 0 & 0 & a \\ 0 & 0 & 0 \\ a & 0 & 0 \\ \end{bmatrix} \quad\text{and}\quad\mathbf u^1 = \mathbf 0\]

Plane strain compression in XZ-Plane

\[\begin{bmatrix} u^5 & u^{2} & u^4 \\ v^5 & v^{2} & v^4 \\ w^5 & w^{2} & w^4 \\ \end{bmatrix}= \begin{bmatrix} a & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & -a \\ \end{bmatrix} \quad\text{and}\quad\mathbf u^1 = \mathbf 0\]

---

6.3 Other

The following boundary conditions would constrain both rigid body rotations and translation while allowing lateral deformation. ‘$*$’ indicates no displacement is prescribed.

Uniaxial tension along X-axis

\[\begin{bmatrix} u^5 & u^{2} & u^4 \\ v^5 & v^{2} & v^4 \\ w^5 & w^{2} & w^4 \\ \end{bmatrix}= \begin{bmatrix} a & 0 & 0 \\ * & * & 0 \\ * & * & * \\ \end{bmatrix} \text{ or } \begin{bmatrix} a & 0 & 0 \\ * & * & * \\ * & 0 & * \\ \end{bmatrix} \quad\text{and}\quad\mathbf u^1 = \mathbf 0\]

Biaxial tension in YZ-plane

\[\begin{bmatrix} u^5 & u^{2} & u^4 \\ v^5 & v^{2} & v^4 \\ w^5 & w^{2} & w^4 \\ \end{bmatrix}= \begin{bmatrix} * & * & * \\ 0 & a & 0 \\ 0 & 0 & b \\ \end{bmatrix} \quad\text{and}\quad\mathbf u^1 = \mathbf 0\]

---

7 Implementation in ABAQUS

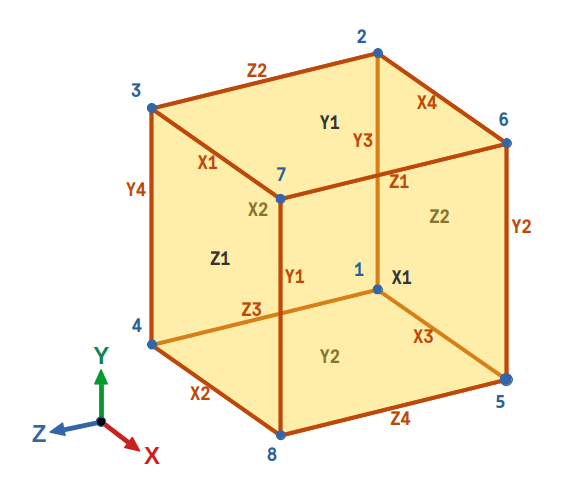Figure 3: node, edge and face numbering for ABAQUS implementation.

7.1 Sample input file for uniaxial tension along X-axis

*Heading
** Job name: sample_tensionX, Model name: cube64
**----------------------------------------------------------------------
** NODAL COORDINATES
**----------------------------------------------------------------------
*Node, nset=cube64, input=nodes.csv
**----------------------------------------------------------------------
** ELEMENTS
**----------------------------------------------------------------------
*Element, type=C3D8, elset=cube64, input=elements.csv
**----------------------------------------------------------------------
** NODE SETS AND ELEMENT SETS
**----------------------------------------------------------------------
*Include, input=sets.data
**----------------------------------------------------------------------
** PBC equations
**----------------------------------------------------------------------
*Include, input=pbc.data
**----------------------------------------------------------------------
** Sections
**----------------------------------------------------------------------
*Solid section, elset = cube64 , material = user_def
1.,
** MATERIALS
**
*Material, name=user_def
*User Material, Constants=0
,
**----------------------------------------------------------------------
** FIXED BOUNDARY CONDITIONS (only zero-valued)
**----------------------------------------------------------------------
** Name: BC-1 Type: Displacement/Rotation (origin-fixed)
*Boundary
c1, 1, 3
** Name: BC-1 Type: Displacement/Rotation (3 corners)
*Boundary
c2, 1, 3
c4, 1, 3
c5, 2, 3
** ---------------------------------------------------------------------
** STEPS
** ---------------------------------------------------------------------
** STEP: Step-1
*Step, name=Step-1, nlgeom=NO
*Static
1., 1., 1e-05, 1. 
** Name: BC-4 Type: Displacement/Rotation
*Boundary
c5, 1, , 0.0005
*Output, field, variable=preselect

7.2 Nodal sets of boundary nodes

** ---------------------------------------------------------------------
**Corners
** ---------------------------------------------------------------------
*Nset, nset=c1
274625
*Nset, nset=c2
274561
*Nset, nset=c3
270401
*Nset, nset=c4
270465
*Nset, nset=c5
4225
*Nset, nset=c6
4161
*Nset, nset=c7
1
*Nset, nset=c8
65
** ---------------------------------------------------------------------
**Xedges
** ---------------------------------------------------------------------
*Nset, nset=edge_x3, unsorted
  270400,  266175,  261950,  ...,   ...,   ...,   ...,
*Nset, nset=edge_x2, unsorted
  266240,  262015,  257790,  ...,   ...,   ...,   ...,
*Nset, nset=edge_x4, unsorted
  270336,  266111,  261886,  ...,   ...,   ...,   ...,
*Nset, nset=edge_x1, unsorted
  266176,  261951,  257726,  ...,   ...,   ...,   ...,
**---------------------------------------------------------------------
** Yedges
**---------------------------------------------------------------------
*Nset, nset=edge_y3, unsorted
  274624,  274623,  274622,   ...,   ...,   ...,   ..., 
*Nset, nset=edge_y2, unsorted
   4224,    4223,    4222,    ...,   ...,   ...,   ...,
*Nset, nset=edge_y4, unsorted
  270464,  270463,  270462,  ...,   ...,   ...,   ...,
*Nset, nset=edge_y1, unsorted
      64,      63,      62,     ...,   ...,   ...,   ...,
**---------------------------------------------------------------------
** Zedges
**---------------------------------------------------------------------
*Nset, nset=edge_z3, unsorted
  274560,  274495,  274430,  ...,   ...,   ...,   ..., 
*Nset, nset=edge_z2, unsorted
  274496,  274431,  274366,    ...,   ...,   ...,   ...,
*Nset, nset=edge_z4, unsorted
    4160,    4095,    4030,    ...,   ...,   ...,   ...,
*Nset, nset=edge_z1, unsorted
    4096,    4031,    3966,    ...,   ...,   ...,   ...,
**---------------------------------------------------------------------
** Xfaces
**---------------------------------------------------------------------
*Nset, nset=face_x1, unsorted
      67,     132,     197,     ...,   ...,   ...,   ...,
*Nset, nset=face_x2, unsorted
  270467,  270532,  270597,  ...,   ...,   ...,   ...,
**---------------------------------------------------------------------
** Yfaces
**---------------------------------------------------------------------
*Nset, nset=face_y1, unsorted
    4291,    8516,   12741,   ...,   ...,   ...,   ...,
*Nset, nset=face_y2, unsorted
    4355,    8580,   12805,   ...,   ...,   ...,   ...,
**---------------------------------------------------------------------
** Zfaces
**---------------------------------------------------------------------
*Nset, nset=face_z1, unsorted
    4227,    4228,    4229,    ...,   ...,   ...,   ...,
*Nset, nset=face_z2, unsorted
    8387,    8388,    ...,    ...,     ...,     ...,

7.3 Linear multi-point constraint equations

**---------------------------------------------------------------------
** Corners
**---------------------------------------------------------------------
*Equation
3
c3,1,1.0,c2,1,-1.0,c4,1,-1.0
*Equation
3
c3,2,1.0,c2,2,-1.0,c4,2,-1.0
*Equation
3
c3,3,1.0,c2,3,-1.0,c4,3,-1.0
*Equation
3
c6,1,1.0,c2,1,-1.0,c5,1,-1.0
*Equation
3
c6,2,1.0,c2,2,-1.0,c5,2,-1.0
*Equation
3
c6,3,1.0,c2,3,-1.0,c5,3,-1.0
*Equation
3
c7,1,1.0,c6,1,-1.0,c4,1,-1.0
*Equation
3
c7,2,1.0,c6,2,-1.0,c4,2,-1.0
*Equation
3
c7,3,1.0,c6,3,-1.0,c4,3,-1.0
*Equation
3
c8,1,1.0,c5,1,-1.0,c4,1,-1.0
*Equation
3
c8,2,1.0,c5,2,-1.0,c4,2,-1.0
*Equation
3
c8,3,1.0,c5,3,-1.0,c4,3,-1.0
**---------------------------------------------------------------------
** edges
**---------------------------------------------------------------------
*Equation
3
edge_y2,1,1.0,edge_y3,1,-1.0,c5,1,-1.0
*Equation
3
edge_y2,2,1.0,edge_y3,2,-1.0,c5,2,-1.0
*Equation
3
edge_y2,3,1.0,edge_y3,3,-1.0,c5,3,-1.0
*Equation
3
edge_y1,1,1.0,edge_y4,1,-1.0,c5,1,-1.0
*Equation
3
edge_y1,2,1.0,edge_y4,2,-1.0,c5,2,-1.0
*Equation
3
edge_y1,3,1.0,edge_y4,3,-1.0,c5,3,-1.0
*Equation
3
edge_y4,1,1.0,edge_y3,1,-1.0,c4,1,-1.0
*Equation
3
edge_y4,2,1.0,edge_y3,2,-1.0,c4,2,-1.0
*Equation
3
edge_y4,3,1.0,edge_y3,3,-1.0,c4,3,-1.0
*Equation
3
edge_z2,1,1.0,edge_z3,1,-1.0,c2,1,-1.0
*Equation
3
edge_z2,2,1.0,edge_z3,2,-1.0,c2,2,-1.0
*Equation
3
edge_z2,3,1.0,edge_z3,3,-1.0,c2,3,-1.0
*Equation
3
edge_z1,1,1.0,edge_z4,1,-1.0,c2,1,-1.0
*Equation
3
edge_z1,2,1.0,edge_z4,2,-1.0,c2,2,-1.0
*Equation
3
edge_z1,3,1.0,edge_z4,3,-1.0,c2,3,-1.0
*Equation
3
edge_z4,1,1.0,edge_z3,1,-1.0,c5,1,-1.0
*Equation
3
edge_z4,2,1.0,edge_z3,2,-1.0,c5,2,-1.0
*Equation
3
edge_z4,3,1.0,edge_z3,3,-1.0,c5,3,-1.0
*Equation
3
edge_x2,1,1.0,edge_x3,1,-1.0,c4,1,-1.0
*Equation
3
edge_x2,2,1.0,edge_x3,2,-1.0,c4,2,-1.0
*Equation
3
edge_x2,3,1.0,edge_x3,3,-1.0,c4,3,-1.0
*Equation
3
edge_x1,1,1.0,edge_x4,1,-1.0,c4,1,-1.0
*Equation
3
edge_x1,2,1.0,edge_x4,2,-1.0,c4,2,-1.0
*Equation
3
edge_x1,3,1.0,edge_x4,3,-1.0,c4,3,-1.0
*Equation
3
edge_x4,1,1.0,edge_x3,1,-1.0,c2,1,-1.0
*Equation
3
edge_x4,2,1.0,edge_x3,2,-1.0,c2,2,-1.0
*Equation
3
edge_x4,3,1.0,edge_x3,3,-1.0,c2,3,-1.0
**---------------------------------------------------------------------
** Faces
**---------------------------------------------------------------------
*Equation
3
face_x1,1,1.0,face_x2,1,-1.0,c5,1,-1.0
*Equation
3
face_x1,2,1.0,face_x2,2,-1.0,c5,2,-1.0
*Equation
3
face_x1,3,1.0,face_x2,3,-1.0,c5,3,-1.0
*Equation
3
face_y1,1,1.0,face_y2,1,-1.0,c2,1,-1.0
*Equation
3
face_y1,2,1.0,face_y2,2,-1.0,c2,2,-1.0
*Equation
3
face_y1,3,1.0,face_y2,3,-1.0,c2,3,-1.0
*Equation
3
face_z1,1,1.0,face_z2,1,-1.0,c4,1,-1.0
*Equation
3
face_z1,2,1.0,face_z2,2,-1.0,c4,2,-1.0
*Equation
3
face_z1,3,1.0,face_z2,3,-1.0,c4,3,-1.0